爆破

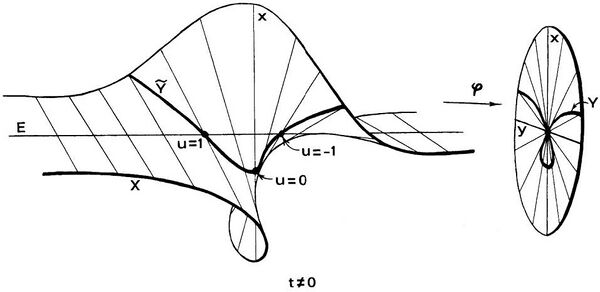
爆破是几何学中的一种构造, 在代数几何中尤为重要. 给定代数簇 $X$ 及闭子簇 $Z\subset X$, 则 $X$ 沿 $Z$ 的爆破 $\tilde{X}$ 是在 $X$ 中将 $Z$ 中每点 $z$ 替换为该点处 $Z$ 的法空间的射影空间, 而得到的新代数簇. 例如, 下图展示了仿射空间 ${\mathbb{A}}^2$ 沿着原点 $\{0\}$ 的爆破. 图中左侧为爆破后的空间, 而右侧为爆破之前的空间. 可以看出, ${\mathbb{A}}^2$ 中每条经过原点的直线都对应爆破后的一条直线, 而原点则被拉开成一条射影直线 ${\mathbb{P}}^1$, 记录经过该点的所有可能的方向. 图中粗线是 ${\mathbb{A}}^2$ 中的一条代数曲线, 它在原点具有结点, 从而不光滑, 但爆破后该曲线变成了光滑曲线.

(图取自 [Hartshorne 1977])

爆破常常视为态射, 即从爆破后的代数簇到原来代数簇的态射. 该态射是双有理态射、射影态射. 该态射下 $Z$ 的原像, 也就是爆破的操作改变的那一部分, 称为例外除子.

爆破在双有理几何中, 特别是奇点消解理论中, 具有重要应用. 奇点消解理论的主要结论说明, 特征 $0$ 域上的任何代数簇都可以通过一系列的爆破, 最终成为光滑的.

1定义

对概形

定义 1.1 (爆破). 设 $X$ 是概形, $\mathcal{I}\subset {\mathcal{O}}_X$ 是拟凝聚理想层. 则 $X$ 沿 $\mathcal{I}$ 的爆破是指概形$${\mathrm{Bl}}_{\mathcal{I}}(X)={\mathbf{Proj}}_X\left(\underset{n=0}{\overset{\infty }{⨁}}{\mathcal{I}}^n\right),$$其中 ${\mathbf{Proj}}_X$ 是相对射影谱, 括号内的部分视为分次环层, ${\mathcal{I}}^n\subset {\mathcal{O}}_X$ 的次数为 $n$.

特别地, 若 $Z\subset X$ 为闭子概形, 则 $X$ 沿 $Z$ 的爆破 ${\mathrm{Bl}}_Z(X)$ 是指 $X$ 沿 $Z$ 的理想层 ${\mathcal{I}}_Z$ 的爆破.

2例子

•	设 $X$ 是代数簇, $Z\subset X$ 是由方程 $f_1=\cdots =f_m=0$ 定义的闭子簇, 其中各 $f_i:X\to {\mathbb{A}}^1$ 是正则函数. 则爆破 ${\mathrm{Bl}}_Z(X)$ 可以视为 $X\times {\mathbb{P}}^{m-1}$ 的闭子簇: $${\mathrm{Bl}}_Z(X)=\{(x,[a_1:\cdots :a_m])\in X\times {\mathbb{P}}^{m-1}|a_i{f}_j(x)=a_j{f}_i(x),\forall i,j\}.$$

3参考文献

•	Robin Hartshorne (1977). Algebraic geometry. Grad. Texts Math. 52. Springer. (doi)

4相关概念

术语翻译

爆破 • 英文 blow-up • 德文 Auflösung (f) • 法文 éclatement (m) • 日文 ブローアップ • 韩文 부풀리기