Cauchy 积分定理
注意区分本文与 “Cauchy 积分公式”、“Cauchy 重积分公式”.
Cauchy 积分定理 (也称为 Cauchy–Goursat 定理) 说明, 复平面上全纯函数的曲线积分在曲线的同伦下不变. 特别地, 全纯函数沿零伦闭曲线的积分为 .
1定理陈述
2定理证明
先建立如下的引理.
引理 2.1 (曲线的折线逼近). 设 是开集, 是可求长曲线, 是连续函数. 则对于任意 , 存在一条 中的折线 , 使得
1. | 有相同的起点和终点, 的顶点都在 上; |
2. | 与 同伦; |
3. | 成立估计式 |
证明. 令 . 作一个紧集 使得 . 因为 在 内是一致连续函数, 故对任意 , 存在 , 使得如果 , 则有 , 其中 是曲线长度. 在 上取分点 , 使得 被这些分点分得的曲线弧长度均小于 , 且 分别是起点和终点. 显见 , 于是把分点连起来得到折线 , 它在 内部.
关于同伦, 可以简单地取直线同伦 . 下面主要证明估计式.
这个引理允许我们把一般的曲线替换为分段可微的曲线 (实际上证明了更强的折线). 当然, 也可以用 Stone–Weierstraß 定理得到.
引理 2.2 (Goursat). 设 是开集, 是一个逆时针旋转的三角形, 则对任意全纯函数 :
证明. 我们通过如下的操作不断把三角形缩小.
这个引理实际上就是 Cauchy 积分定理对三角形的特殊情况. 据此, 不难推出 Cauchy 积分定理对矩形也成立.
引理 2.3. 设 是圆盘, 是全纯函数, 则 在 内存在原函数, 即存在全纯函数 使得对任意 : 此时, 对分段可微曲线 , 有
证明. 先证明第一个命题. 不失一般性, 假设 的圆心是原点. 对任意 , 考虑下图所示的折线 :
定义我们来证明这就是 的原函数. 为此, 需要计算 . 同时做出 :
首先, 根据引理 2.2, 因为矩形上的积分为零, 所以 上的积分比起 多出来的是从 到 再到 的折线上的积分; 再因为三角形上的积分为零, 这段积分还等于 到 的线段上的积分. 记这条线段是 , 则因为 是连续的, 所以 , 其中 . 此时进一步: 当 时, 上式为 , 即 . 也就是 . 第一个命题得证.
定理 1.1 的证明. 根据引理 2.1, 可不妨设 分段可微. 设它们之间有同伦 , 并令 . 是紧集 上的连续函数, 其像 也是紧集.
由 的紧性, 取 , 使得任何以 中的点为中心, 为半径的圆盘都在 内.
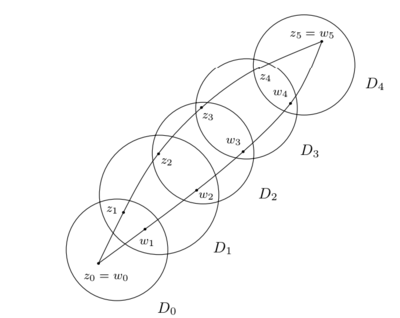
因为 是一致连续函数, 对上述 , 可以找到 使得只要 , 就有对任何上述 , 找一组半径为 的圆盘 , 以及分别位于 上的两组点 , 使得 分别是 的起点和终点, 且例如, 下图展示了 的情况.
这些圆盘都包含在 内. 对每个 , 其内部可以找到 的一个原函数 , 这是因为引理 2.3 . 在 中, 是同一个函数的两个原函数, 所以相差一个常数. 于是也就是这导致
也就是 .
3推论
原函数
在之前的引理中提到, 在圆盘内全纯的函数总有原函数, 并且证明了类似于 Newton–Leibniz 公式的结果. 证明了 Cauchy 积分定理以后, 这种结论能被推广至单连通集合.
命题 3.1 (原函数). 设 是单连通开集, 则任何 的全纯函数都有原函数.
单连通的条件是不能去掉的. 比如: 在 全纯, 如果它存在原函数, 则对内部包含原点的光滑曲线 有 ; 但是这个积分等于 , 矛盾. 出现问题的原因在于 不是单连通的.
4相关概念
术语翻译
Cauchy 积分定理 • 英文 Cauchy’s integral theorem • 德文 cauchyscher Integralsatz (m) • 法文 théorème intégral de Cauchy (m)