Pascal 定理

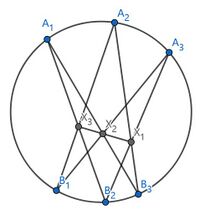
Pascal 定理是个射影几何定理, 说的是圆锥曲线上的三对点如下图般交叉连线, 产生的三个交点共线.

1陈述

定理 1.1. 圆锥曲线 $\Gamma$ 上有六个点 $A_1,A_2,A_3$, $B_1,B_2,B_3$. 分别以 ${\ell }_1,{\ell }_2,{\ell }_3$ 记直线 $A_2{B}_3,A_3{B}_1,A_1{B}_2$, 以 $m_1,m_2,m_3$ 记直线 $A_3{B}_2,A_1{B}_3,A_2{B}_1$, 再以 $X_1,X_2,X_3$ 记交点 ${\ell }_1{m}_1,{\ell }_2{m}_2,{\ell }_3{m}_3$. 则 $X_1,X_2,X_3$ 共线.

2证明

用坐标几何

在坐标平面考虑问题, 并以曲线的字母表示定义它的多项式. 具体地说, 以 $\Gamma$ 表示二次多项式, 使得方程 $\Gamma =0$ 定义圆锥曲线 $\Gamma$, 六条直线类同. 把两组三条直线的定义多项式乘起来, 得到两个三次多项式 ${\ell }_1{\ell }_2{\ell }_3$ 与 $m_1{m}_2{m}_3$. 由于这两组三条直线不同, 这两个三次多项式线性无关. 由条件, 它们都在 $A_1,A_2,A_3$, $B_1,B_2,B_3$, $X_1,X_2,X_3$ 为零. 任取点 $C\in \Gamma$ 异于 $A_1,A_2,A_3$, $B_1,B_2,B_3$, 然后适当取不全为零的系数 $\lambda ,\mu$ 使得 $\lambda {\ell }_1{\ell }_2{\ell }_3+\mu m_1{m}_2{m}_3$ 在 $C$ 处为零. 现在三次多项式 $\lambda {\ell }_1{\ell }_2{\ell }_3+\mu m_1{m}_2{m}_3$ 与二次多项式 $\Gamma$ 有至少七个公共零点: $A_1,A_2,A_3$, $B_1,B_2,B_3$, $C$. 由于 $7>3\times 2$, 这说明它们有公因子. 由于 $\Gamma$ 是圆锥曲线, 并非两条直线, 为不可约, 所以只可能是它整除 $\lambda {\ell }_1{\ell }_2{\ell }_3+\mu m_1{m}_2{m}_3$. 于是设$$\lambda {\ell }_1{\ell }_2{\ell }_3+\mu m_1{m}_2{m}_3=f\Gamma ,$$则 $f$ 为一次多项式, 零点集为直线. 上式左边在 $X_1,X_2,X_3$ 为零, 而由于圆锥曲线和直线只能交两个点, $\Gamma$ 在这三点不为零, 所以只有 $f$ 在这三个点为零, 即 $X_1,X_2,X_3$ 共线.

注 2.1. 这里用到 $\Gamma$ 不可约. 当 $\Gamma$ 是两条相异直线相乘时, 在上述证明中取 $C$ 为两线交点, 不难得到同样的结论. 这就是 Pappus 定理.

注 2.2. 由此可见 Pascal 定理在任何域的射影平面上都成立.

用 Euclid 几何

利用射影变换, 实际上只需证明圆锥曲线为圆的情形. 为了证明 $X_1,X_2,X_3$ 共线, 实际上只需要证明 $\angle A_1{X}_2{X}_3=\angle B_3{X}_2{X}_1$, 或者 $\angle B_1{X}_2{X}_3=\angle A_3{X}_2{X}_1$. 注意到下面的引理:

引理 2.3. 设 $\alpha ,\beta ,\gamma ,\delta >0$, 满足 $\alpha +\beta =\gamma +\delta <\pi$. 如果$$\frac{\sin \alpha }{\sin \beta }=\frac{\sin \gamma }{\sin \delta }$$则 $\alpha =\gamma ,\beta =\delta$.

引理的证明是基本的三角运算. 根据引理, 只需要证明$$\frac{\sin \angle A_1{X}_2{X}_3}{\sin \angle B_1{X}_2{X}_3}=\frac{\sin \angle B_3{X}_2{X}_1}{\sin \angle A_3{X}_2{X}_1}$$根据正弦定理:$$\frac{\sin \angle A_1{X}_2{X}_3}{\sin \angle X_2{A}_1{X}_3}=\frac{A_1{X}_3}{X_2{X}_3},\frac{\sin \angle B_1{X}_2{X}_3}{\sin \angle X_2{B}_1{X}_3}=\frac{B_1{X}_3}{X_2{X}_3}$$于是$$\frac{\sin \angle A_1{X}_2{X}_3}{\sin \angle B_1{X}_2{X}_3}=\frac{A_1{X}_3}{B_1{X}_3}\cdot \frac{\sin \angle X_2{A}_1{X}_3}{\sin \angle X_2{B}_1{X}_3}$$进一步, 根据圆的性质$$\frac{A_1{X}_3}{B_1{X}_3}=\frac{A_1{A}_2}{B_1{B}_2},\frac{\sin \angle X_2{A}_1{X}_3}{\sin \angle X_2{B}_1{X}_3}=\frac{B_2{B}_3}{A_2{A}_3}$$所以$$\frac{\sin \angle A_1{X}_2{X}_3}{\sin \angle B_1{X}_2{X}_3}=\frac{A_1{A}_2\cdot B_2{B}_3}{B_1{B}_2\cdot A_2{A}_3}$$同理可证得 $\frac{\sin \angle B_3{X}_2{X}_1}{\sin \angle A_3{X}_2{X}_1}$ 也是此值.

用 3D 几何

Dandelin 的三维证明利用单叶双曲面来提升问题至三维空间. 具体步骤如下:

在给定的单叶双曲面上, 取其两组母线分别为红线和蓝线.

从中选择各三条交替颜色的直线构成一个非平面六边形.

每个顶点处构成的角平面 (由该顶点两边确定) 与对应对角顶点的角平面相交于一条直线.

当用平面与双曲面相交得到圆锥曲线时, 这些角平面交线正好落在平面上, 从而证明了对边交点共线.

用射影几何

采用射影变换保持交比的证明如下:

四元组 $ABCE$ 从点 $D$ 投影到直线 $AB$ 得到四元组 $ABPX$,

四元组 $ABCE$ 从点 $F$ 投影到直线 $BC$ 得到四元组 $QBCY$.

因此有$$R(AB;PX)=R(QB;CY),$$这两个四元组中的一个点 $B$ 重合, 所以连接其他 3 组对应点的直线$$AQ,PC,XY$$必共点, 从而得出 $X,Y,Z$ 共线.

用椭圆曲线的群结构

$\Gamma$ 与直线 $X_1{X}_2$ 的并集为一条退化的椭圆曲线, 椭圆曲线的群结构具有结合律, $(A+B)+C=A+(B+C)$, 故 $A,B+C,(-A-B)-C$ 三点共线

3相关概念

•	Brianchon 定理是其对偶.

•	Pappus 定理是其退化情形.

•	Cayley–Bacharach 定理是其推广.

术语翻译

Pascal 定理 • 英文 Pascal’s theorem • 德文 Satz von Pascal • 法文 théorème de Pascal • 拉丁文 theorema Pascalium